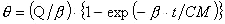1. 前言
机械构造中的平台进给系统是决定轴方向精度的重要的运行机构。
随着NC机床精度的提高和现在半导体制造设备、信息相关设备、超精密加工的发展，市场中不断提出高精度的要求。
在这里，将会以机构里面重要的机械要素——滚珠丝杠、直线引导装置为中心，对各要素对定位精度的影响进行概述。
2. 精密定位精度的因素
图1展示的是精密定位机构中的构成要素。虽说为定位精度，但需要的功能和精度是多种多样的，因此使用的要素也要考虑多种组合。并不是哪个要素一定是好的，而是为了达到要求的功能和精度，哪个要素是合适的。
另外，控制驱动装置当然也发挥着极为重要的作用。提高定位系统的高精度化，并不是针对某单一要素的高精度化，关键在于对系统整体进行探讨和最优化设计。
其中，传送螺纹作为使用的传送机构的要素之一，被业界内广泛使用。按照精度，要素分类多种多样。从便宜的滑动丝杠，到超精密角丝杠以及静压丝杠。
在细微定位方面，压电元件、直线电机等直接驱动或摩擦驱动装置等都具有各种实用化的案例。
虽然有各种各样的传送驱动要素，但从价格、长时间的稳定性、行程・刚度・负载容量・速度的响应性、控制的难易程度、使用的便利性等方面进行考虑，滚珠丝杠拥有诸多特长。
引导机构中会利用各种的要素，其中滑动引导（动压引导）是最常见的。但在现今高精度高速度化的要求下，受到引导部位的游隙、摩擦力随速度、外力的变化、低速时的粘滑、高速时的耐久性等问题的影响，静压引导和滚动引导的使用在逐渐增加。另外在真空等环境下磁悬浮引导也逐渐进入实用阶段。
3. 滚珠丝杠定位精度的影响因素
3.1. 导程精度
滚珠丝杠的导程精度是1980年制成了JIS标准，1987年进行了部分订正，规定了（1）累计代表移动量误差、（2）相对丝杠部分有效长度的最大幅度、（3）任意300mm的最大幅度、（4）任意一圈转动的最大幅度等共4个特性。
虽然滚珠丝杠要求的功能是螺母的进给精度，但一般对轴单体的导程精度进行测量的情况比较多。导程精度分为广范围和狭范围，相对来说，广范围精度因为加工精度好和容易补正的原因，很少出现问题。今后为了应对高精度化的需要，狭范围精度会越发重要。
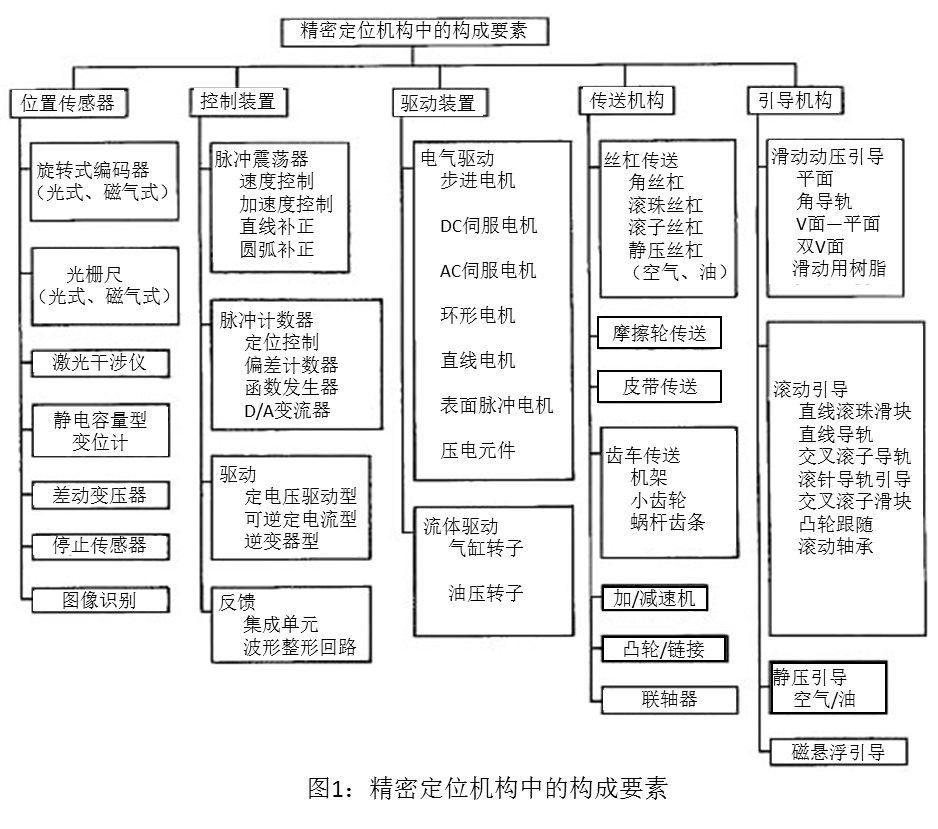
图2是最高精度C0级的导程误差的一个示例。累计代表移动量误差是1μm/208mm，相对丝杠部分有效长度的最大幅度是2μm，螺母组装状态的最大幅度不超过0.9μm，是规格值的1/2以下。
误差变动的特征成分是沟道磨床中轴的1圈转动的成分（12mm周期），虽然单体是1～1.5μm，但因为螺母组装后的平均化效果会减少到0.5μm以下。一般相比单体的狭范围的误差，螺母组装后有1/2到1/3的减少。
3.2. 非同期成分
上述的导程精度即使周期不一样，均会出现轴的旋转同期成分。滚动要素中由于会出现滚动体的自转/公转所产生的非同期成分，在超精密的领域会成为主要问题。原因在于滚道面的粗糙度、真圆度、滚动体外径之间的相互差、真球度不良等，更有循环机构引起的滚动体在出入过程中引起的振动问题。根据塚田等1)的报告，在一个移动误差在0.4～0.5μm的平台上，将原本使用的滚珠丝杠使用保持架或者合成树脂的间隔钢球，移动误差将会降低至0.1μm以下。钢球通过成分不单会通过振动的形式出现，还会通过扭矩变动的形式出现，这容易引起电机输出扭矩的移动误差。这类误差不同于同期成分，很难通过控制补偿来补正，而且出现在滚珠丝杠应用在超精密领域的时候，正确的评价研究案例很少，是今后的重要课题之一。
3.3. 安装部精度、安装误差
即使导程精度是高精度的，如果不正确进行安装，定位精度也会变差。1987年的JIS订正中，认识到了滚珠丝杠安装部精度的重要性，因此规格值比以前变更的更为严格，并且今后会有更加严格的趋势。
如果滚珠丝杠、轴承和引导机构的同心度差，就容易出现旋转跳动的误差，容易和导程误差混淆。根据米田2）的案例报告，将螺母和支撑轴承的同心度控制到原来的数分之一，超精密切削时的导程误差特征将会消失。
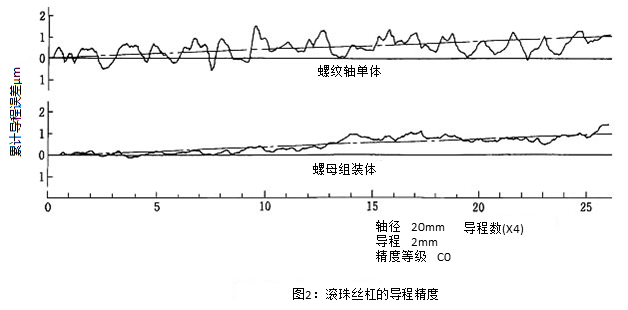
图3展示了在空气静压导轨的引导下，C0级滚珠丝杠通过联轴器连接，移动时的位置变化测量示例3）。虽然出现了回转振动成分，但幅度很小。并且，在要进一步减少时，将螺母与平台只在轴方向上固定，其他方向自由的安装方法也已经在实际中得到应用4～7）。
3.4. 刚度
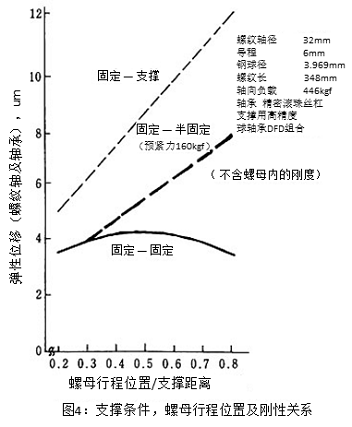
如果滚珠丝杠整体的刚度弱，就会发生空程。滚珠丝杠整体的刚度并不只是螺母内部刚度（钢球和沟道之间的刚度），还有丝杠轴的伸缩、支撑轴承的刚度等因素，需要整体进行考虑。一般丝杠轴的伸缩占的比例最大，该刚度受的支撑条件影响很大。
如图4所示，固定—支撑（轴方向自由）时，随着螺母位置，刚度的变化较大，固定—固定时的刚性较高，且变化更小。
固定—固定的条件下虽然对高精度化更有利，但也有因为丝杠轴热膨胀而使支撑轴承过负载等问题。这种时候使用固定—半固定的构造比较多8)。
3.5. 摩擦力矩
滚珠丝杠的摩擦本来就很小，感觉上可以为了提高刚度而加大预紧力。但是，在精密定位方面，因为滚珠丝杠和支撑轴承的扭矩（特别是摩擦力矩波动）变化引起的控制系统累计脉冲的变动，会引起定位精度的误差。因此摩擦力矩的稳定越来越很重要，在1987年JIS订正中对摩擦力矩的规格进行了定义，对基准例句Tp和相对基准例句的变化规格值进行了规定。
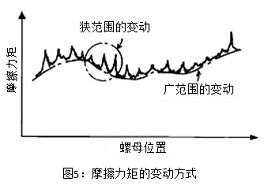
摩擦力矩的变动也有广范围和狭范围的变动。广范围变动的原因主要是因为丝杠轴沟道径的误差而引起的预紧量的变化（定位预紧的情况）。如果刚度没有问题，使用定压预紧时这种变化会变得非常小。狭范围变动是由丝杠轴沟道面的精度、形状精度、循环路的设计/加工精度等因素引起的。狭范围变动在低速和摇动时特别明显，使用间隔钢球对改善狭范围变动有很好的效果。
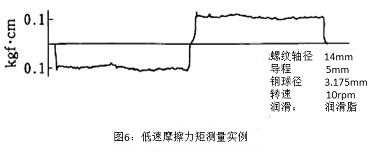
相比滑动丝杠，滚珠丝杠被认为摩擦力矩小但变动大，但如图6所示，现在已经已经有了很大的改善。
如同后面会论述，在高速运转时，润滑剂粘度的影响会使摩擦力矩增大。相反超低速运行时，润滑剂的特性会对摩擦力矩产生影响。
如前面所述，滚珠丝杠的安装误差也会与摩擦力矩变动有关系。如果安装精度差，伴随着钢球通过成分的变化，摩擦力矩随着扭转力的增大而增大，特别在低速领域会有摩擦力矩异常增大的情况发生。
3.6. 热膨胀
随着高速化的推进，滚珠丝杠热变形的影响越来越大。
滚珠丝杠的温度上升可以通过质点系的简化而用以下计算公式求出。
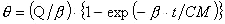
在这里，
- θ：温度上升 (°C)
- t： 时间 (h)
- Q： 单位时间内的发热量 (kcal/h)
- β：单位时间单位温度内的放热量 (kcal/h・°C)
- CM：热容比 (kcal/°C)
热变形可以通过热膨胀系数和温度上升值而求出。
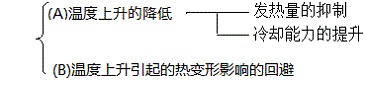
以下整理出热变形的对策。
在考虑实际的机械的发热量时因为电机和支撑轴承的发热也很大，不能只考虑滚珠丝杠的影响。这里只针对滚珠丝杠单体的影响进行考量，影响因素有摩擦力矩和转速。
摩擦力矩由负载项T
F和速度项T
V的和组成。滚珠丝杠的受力由预紧力和外部载荷组成，但预紧滚珠丝杠的外部载荷影响小，因此T
F的计算中只计算预紧摩擦力矩是没有问题。如前说述，即使预紧量增大，全体体系的刚度也不会明显增加，所以预紧力的设定以最小限度为好。
速度项T
V是由润滑剂的粘着抵抗和搅拌抵抗而产生的摩擦形成的。粘度对T
V的影响很大，因此润滑剂的选择非常重要。笔者考虑了润滑性能，在轻负载・轻摩擦力矩领域里推荐使用40℃（基油）粘度的10～30cSt，在大负载领域里推荐使用35～50cSt的润滑剂。
转速与发热量成正比。但是，因为散热量也和转速有关系，因此温升与转速的0.5次方成比例。无论如何，低转速温升较低，因此伴随着高速化也有导程加大的倾向。
发热量由取决于以下几方面的和（1）滚珠丝杠表面的热传递、（2）向丝杠轴端的热传递、（3）螺母向螺母座的热传递、（4）强制冷却的散热 。
如上述所说，通过选择适合的预紧量和润滑剂，可以有效地抑制温升。为了今后进一步高速化，要考虑使用一些强制冷却手段。
强制冷却有各种各样的方法，冷却对象分为螺母和丝杠轴。螺母冷却因为不是直接对丝杠轴进行冷却，冷却效果较小，轴冷却的效果比较好。在丝杠轴外周或中空轴冷却都在实际应用上没有问题。冷却流体按效果排序分别是水、油、空气。虽然空气因为流量的原因冷却效果较小，但因为有流体不用回收等优点也有使用。中空滚珠丝杠作为强制冷却用滚珠丝杠已经进行了系列化，各种效果也已经作成了各种报告。
回避温升的影响的方法也有各种各样的提案。用低膨胀系数的材料来制作丝杠轴可以减少热变形，但是材料强度、成本等因素在应用时要优先考虑。
最常使用的方法是丝杠轴的预拉伸。但是在轴旋转的情况下，一般考虑温升2～3°C相当的预拉伸力，特别情况也有考虑5°C相当的预拉伸力。前述的强制冷却和预拉伸力一起使用在不必考虑高精度冷却能力的时候非常有效果。
根据垣野
9)的报告，也有通过实时监察电机上的负载和速度，预测温升和丝杠轴热变形，从而进行补正的方法。
闭环控制时，热变形并不会产生直接的影响。虽然这是高精度化的有效方法，但因为成本上升和控制困难等原因也并不是万能的。
4. 直线引导装置的影响
如前说述，有各种各样的直线引导装置。因为近年滚动引导滑块有很多使用案例，这里主要对交叉滚子导轨（非循环滚子类型）、直线导轨（循环球类型）引起的定位精度的相关问题进行阐述。
4.1. 交叉滚子导轨
4.1.1. 安装和安装精度
这种直线引导是由导轨与基台组装，调整间隙后得到相应的性能的。所以如果不进行正确的安装就不能得到高精度的引导，必须十分地注意安装方法。
导轨的沟道面的粗糙度和弯曲固然已经很小，但沟道的垂直度和形状也很重要。因为滑块的安装面最后是通过无间隙地安装导轨得到的，所以要得到高精度的运行精度就必须使导轨精度达到同等级的精度。通常通过横压螺钉来调整组装后的压紧力，但在拧紧螺钉时会使导轨变形，从而使运行精度恶化。因此会在导轨和横压螺钉之间放入横压版，使螺钉力得到平均化。
4.1.2. 运行精度
这种类型的引导如果得到正确的组装，将会得到良好的运行精度。
交叉滚子导轨（其他非循环导轨同理）随着平台的位置变化，支撑的滚动体的位置是相对移动的，因此预紧量和刚度在变化，运行精度也会变差。所以希望滚动体部分的全长比最大的行程要长。因为滚子径的相互差会引起运行精度在狭范围内的变动和使非同期成分的产生，依据笔者的经验，如果上述的滚子部全长变长，可以得到平均化效果，对运行精度也有影响。
根据这样的对策，行程350mm的平台的水平/垂直方向的直线度可以达到0.6μm，垂直转向达到1.9秒，偏转转向达到0.5秒。
4.1.3. 微小滑动
这样的非循环型直线滑块外形小，并且和循环型相比没有因循环引起的非同期变动成分，适合高精度使用。
但是，非循环型直线滑块也有缺点，其中之一就是微小滑动这一现象。这个现象是在平台往复运动的过程中保持架相对与导轨的相对位置会一点一点地偏移，最终保持架会脱离出导轨。虽然导轨的两端会安装止动装置，但保持架会撞到止动装置造成运行精度不良，也会产生保持架破损。
作为对策，有尝试使用齿轮架或者钢丝等来矫正导轨和保持架的位置，但结构很复杂，这个特性的类型也会损坏。
笔者在详细地对微小滑动进行实验确认之后发现，在滚子和导轨都保持着正常精度的情况下，微小滑动容易因为预紧不均匀和润滑性能过于良好而引起，相反，对滚子进行特殊的表面处理可以抑制这种现象。并且在一般的使用范围内，微小滑动现象可能不会发生。但是，在平台负载运动的情况下会造成预紧不均匀的现象，所以需要注意，要像前文说述一样尽量加长滚子部位的长度，使载荷得到平均化。
4.2. 直线导轨
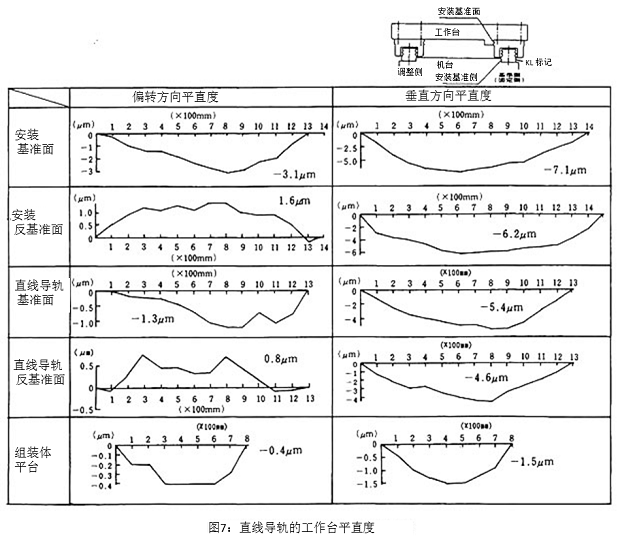
直线导轨因为导轨很长，导轨的精度最后由导轨安装面的形状来决定。所以必须制造高精度的引导面，使得引导面的平直度、安装面之间的平行度都高精度化。这种情况下，安装面的粗糙度并不是问题，形状精度才是重要的，所以并不是必须使用研磨加工。
虽然基本情况下引导面的精度会影响安装面精度，但现实中受导轨和滑块之间的相互干涉、接触部位的变形等平均化效果的影响，安装面精度的影响会降低到1/2～1/10。图7是从安装面精度到安装体精度的测量示例，可以明显看出上述现象。
特别是在安装面经过削刮加工后达到1～2μm粗糙度后，用治具测量的例子中，垂直转向达到0.2μm/360mm ，偏转转向达到0.8μm/390mm，得到了逼近静压引导的高精度。
直线导轨（其他滚动体循环类型同理）有向平直度这样的广范围变动，也有滚动体循环关联的狭范围变动。
狭范围变动的原因之一是螺钉锁紧引起的误差。这是因螺钉固定的锁紧力导致导轨和导轨沟道的变形而引起的。这种误差的消除，可以通过使加工的安装时的螺钉锁紧力等于实际使用时的锁紧力，再进行沟道研磨来解决。
还有一个原因，是钢球在出入负载圈过程中引起的钢球通过成分。这种成分是因为倾斜误差引起的，所以在加工点在平台的悬垂点时会增大，是一种平直度的狭范围变动。
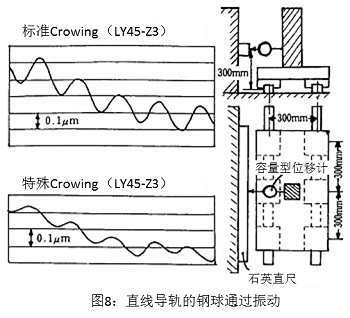
这种变动是因为钢球在出入负载圈时引起的，为了使钢球顺滑地出入负载圈，可以把滑块沟道的端部设计成缓缓倾斜的形状（Crowning），使这种变动减少。这种变动在预紧大的时候变动值会变大，并且和滑块单体相比，平台安装后因为平均化的效果变动会变得很小。
所以，为了减小这种变动，提高钢球接触部位的刚度，设计出预紧力引起弹性变形小的沟道形状（公海赌赌船jcjc710-LY型）；适当地设计Crowning的型状；从整体设计的角度出发，因为误差会随着角度扩大，所以为了控制悬垂量，滑块之间要设计足够的跨距；预紧力设计在最小限度；滑块数增加提高平均化效果等等。如图8的测量示例所示，标准品在悬垂300mm位置的变动量是0.16μm，特殊Crowning使用后可以得到0.07μm以下的变动量。
5. 定位精度的测量示例与原因分析
定位精度这样的词语使用非常广泛，到底如何定义还没有明确的规定。一般来说美国机床工业协会的提案被最广泛地使用。
这种考虑方法是，由任意一点，重复7次进行同一方向的定位，得出的数据中计算出平均值X和离散程度σ，定义以X为中心偏差±3σ， 即
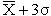和
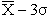范围内的最大/最小值为系统精度，同时定义±3σ是重复精度。这个方法初看很合理，但只有在实际误差符合正态分布的时候才合适，在误差是有特殊规律的时候则是错误的。并且，只有这种评价方法的时候误差的原因分析也很困难。
笔者这里介绍别的随着平台的连续移动测量，从出现的周期性规律力评价误差原因的手法。
5.1. 机床的定位精度测量
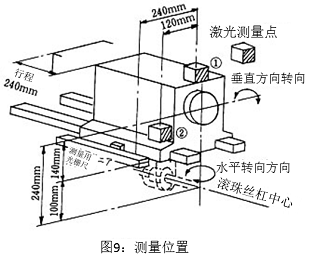
对一台半闭环控制的机床中使用光栅尺进行测量，得出很大的误差（30～40μm/240mm）。为了寻找原因，使用激光测长仪对定位精度，姿势精度进行测量。测量点如图9所示。
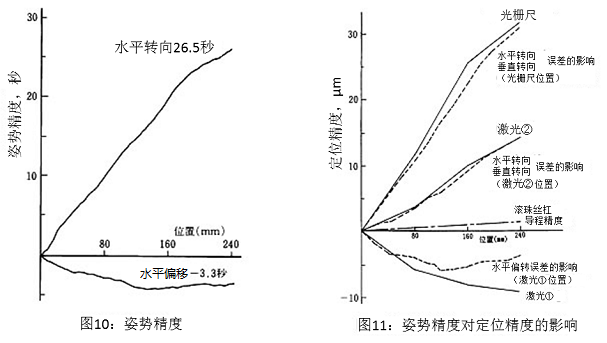
图10表示平台的垂直转向精度和水平转向精度，特别是水平转向精度的误差很大。图11表示各个测量点中用光栅尺和激光测长仪测量定位精度的结果，用实线表示。各个测量点的结果有很大不同。计算出包括所有位置误差从图10所示的姿势精度在内的各个测量点的所有位置误差，再加上滚珠丝杠的导程精度的值，在图11中用虚线表示。可以看出，这和定位精度基本一致，但是，如点划线所示滚珠丝杠的导程误差非常小，定位精度基本由姿势精度而决定。
一般平直度作为平台的姿势精度来测量的情况很多，在行程比较小的场合，测量结果只有4μm，虽然往往被误解为精度很高，但也能了解这对定位精度的影响很大。
平台的姿势精度受定位精度的影响很大，并且在广范围的变动误差中温度上升对姿势精度也有很大程度的影响。
在全闭环控制的时候姿势精度的影响也会出现，比如使用光栅尺对位置进行控制时平台中心会有大的定位精度误差存在。
5.2 空程的评价
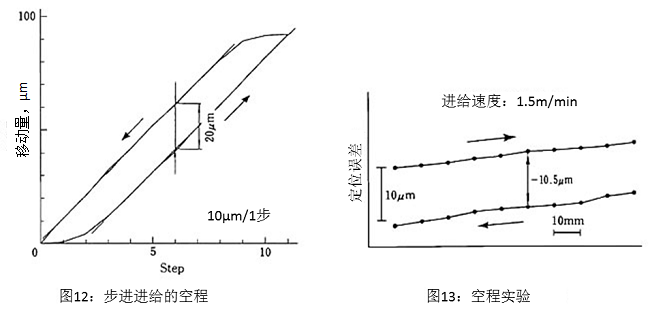
图12展示了NC机械步进进给的结果，产生了20μm的空程。使用同样的机器，不断增大运送速度进行测量，如图13所示，空程量为负（移动过了）。这是因为启动时相对于指令实际的运动有所延迟，因此停止时出现了超程。
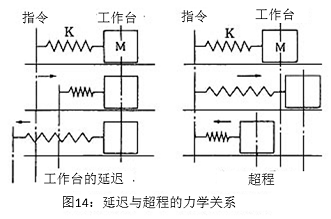
图14是建立了延迟和超程状态的力学模型。如模型所示，延迟和超程在力学上都是同一个关系，所以往复的空程是启动时的延迟或停止时的超程的2倍。现在，如果只出现延迟而不出现超程，将会成为图12一样的空程，如图13所示相比延迟超程的误差较大。
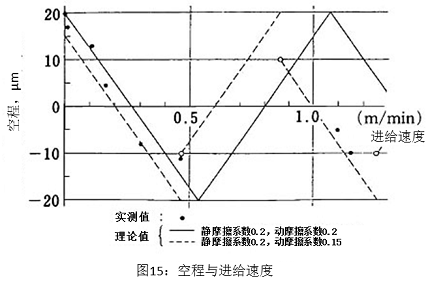
超程由于根据停止时的力学状态会发生变化，平台模型假定为1自由度的弹簧质量模型，求出运送速度和空程的关系，并与实测值做比较，如图15所示。可以看出，计算值和实测值比较吻合。
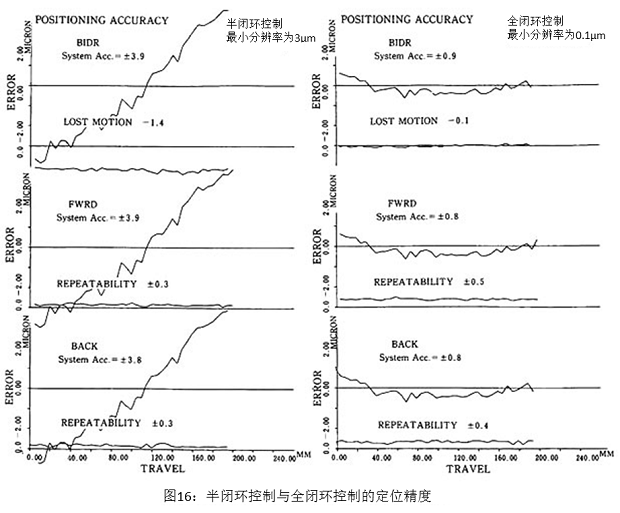
5.3. 小型平台的测量
图16是精密定位平台中半闭环控制和全闭环控制下的定位精度的测量示例。这个平台由滚珠丝杠（导程3mm）和交叉滚子导轨构成，半闭环的编码器是1000分度/1转，全闭环是使用分辨率为0.1μm的光学光栅尺。测量结果显示，即使把测量误差包括在内，也具有较高的精度。
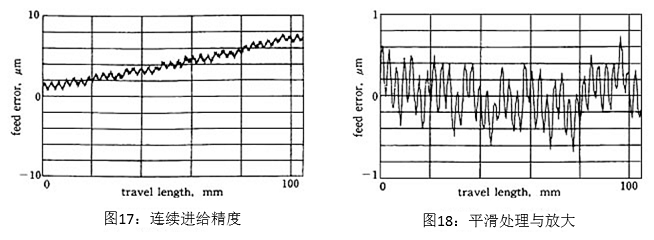
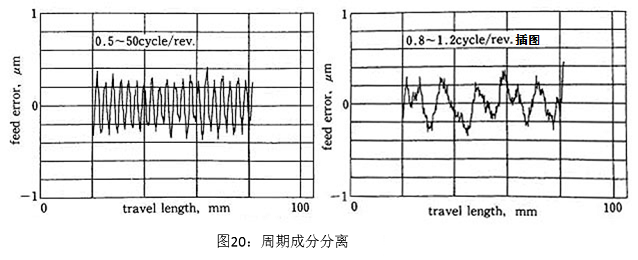
虽然这种评价方法评价讨论此平台具有何种水平的精度，但无法知道此精度内包含了怎样的误差要素。为了探讨误差原因，如图17所示，为测量连续进给进度的结果。测量方法是触发电机内藏的编码器，1转中采集100点数据，发现出了周期性的误差成成分。为了分析这个狭范围变动成分，将数据经过倾斜补正后，通过平滑处理（移动平均），纵轴扩大处理后得到图18的图形。这次测量虽然使用了激光测长仪，但一位微小振动或空气状态等环境因素有±0.1～0.2μm的波动。为了消除这种成分对数据进行了平滑处理。
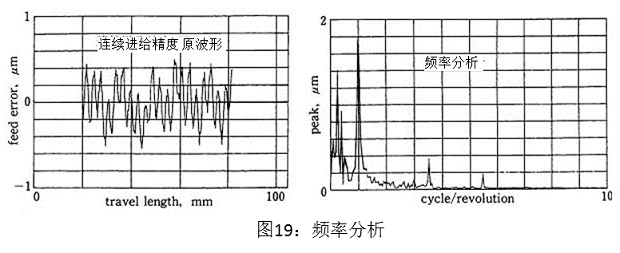
图19展示了对原波形的一部分进行频率分析的结果。从图中可以得知，在0.25～0.4cycle/rev.和1cycle/rev.附近有特征频率出现。图20是通过逆傅立叶变换滤波了0.5cycle/rev.以下的频率的成分之后的结果。高频成分包含在内，周期3mm（1转）的成分几乎占了全部。即使考虑这次测量使用的编码器的1转的累积误差为基本分辨率的1/10，也会存在每转0.3μm的周期误差。实测的误差是0.5～0.7μm，至少一半以上是编码器的误差，剩下的推测是滚珠丝杠振动回转产生的误差和导程误差。
图20为逆转1周且滤掉了周期成分（0.8～1.2cycle/rev.）的结果。出现了高频成分的乱波，周期12mm（0.25cycle/rev.）的成分为0.5～0.6um。这个成分与螺纹磨床的螺纹导程一致，因此认为是由于滚珠丝杠的导程误差引起的。可以根据分析连续进给精度的周期性，分离出各要素的误差，进行评价。
6. 后记
以滚珠丝杠和滚动引导装置对定位精度的影响因素进行了讨论。
今后考虑超精密定位的课题时，可以确立各种各样的有意义的课题。
本文没有对运动响应问题进行论述。如果有机会，会讨论高加减速响应和2轴定位的周期精度。
本报告只限定讨论定位精度，但实际使用过程中，清洁环境、真空环境、非磁性环境或高速化下带来的振动、噪音等也是一个课题。
如果本文由内容不充足或者语言不到位的地方，请指出。如果本文能在定位机构因素的技术上贡献微薄之力，本人也会倍感到荣幸。
参考文献：
- 1) 塚田， 其他：精密机械设计便览，98，（社）精机学会
- 2) 米田：应用机械工学，1984年5月刊，98~103
- 3) 相泽，其他：公海赌赌船jcjc710 Technical Journal, N0646,(1986)54
- 4) 田中：应用机械工学，1987年8月刊，110~116
- 5) 大野木：机械技术，第35卷9刊，（1987）77~83
- 6) 木村，其他：机械技术，第35卷9刊，（1987）115~121
- 7) 高桥：应用机械工学，1987年4月刊，104~109
- 8) 二宫：超精密传送定位机械的设计·评价，75~85，TRICEPS（1987）
- 9) 垣野，其他：精密工学志，第54卷9刊，（1988）131~136
- 10) NMTBA：DEFINITION AND EVALUATION OF ACCURACY AND REPEATABILITY FOR NUMERICALLY CONTROLLED MACHLNE T00LS
- 11) 山口，其他：公海赌赌船jcjc710 Bearing Journal, No.640, (1980) 35～49
